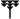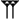El Sistema Babilónico (Base 60)

El sistema de numeración utilizado por la civilización babilónica (alrededor del 2000 a.C.) es un sistema sexagesimal (base 60) y posicional, similar a nuestra base 10, pero utilizando potencias de 60. Es el origen de la división moderna del tiempo (60 minutos, 60 segundos) y los ángulos (360 grados).

1. Símbolos Fundamentales (Base 10 auxiliar)

Dentro de cada "dígito" de base 60, los números del 1 al 59 se construyen usando una combinación de solo dos símbolos básicos:

Unidad (1)

Decena (10)

Cero (0)

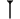
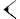
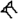
Para representar números como el 43, simplemente se concatenan los símbolos de la decena y la unidad: el 40 y el 3.

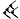
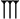
2. Valor Posicional (Base 60)

El valor total de un número se determina por la posición del dígito de base 60, de derecha a izquierda:

• Posición 1 (Derecha): Unidades simples (× 60⁰ = × 1)
• Posición 2: Sesentenas (× 60¹ = × 60)
• Posición 3: Trescientos-Sesentenas (× 60² = × 3600)
• Posición 4: Doscientos-Diez-Mil-Seiscientas (× 60³ = × 216000)

🔢 Conversión de Arábigo a Babilónico (Ejemplo: 4625)

Para convertir el número arábigo 4.625 a babilónico, utilizamos la división sucesiva por la base (60):

El número babilónico (en base 60) es la secuencia de restos leída al revés: (1, 17, 5).

|

|

🏺 Conversión de Babilónico a Arábigo (Ejemplo: 1, 17, 5)

Multiplicamos cada dígito de base 60 por su valor posicional (la potencia de 60) y sumamos los resultados:

Dígito 1 (Izquierda): 1 × 60² = 1 × 3600 = 3600

Dígito 2 (Medio): 17 × 60¹ = 17 × 60 = 1020

Dígito 3 (Derecha): 5 × 60⁰ = 5 × 1 = 5

Resultado final: 3600 + 1020 + 5 = 4625